
Standard Form to Factored Form
Standard Form: 0= ax² + bx + c
Factored Form: y=a(x-r)(x-s)
0= n² + 14n + 48
-Well first you need to figure out two numbers that add to 14 and also multiply to 48
14= (12+2) (8+6) (13+1) (10+4)
48= (12x4) (48x1) (8x6)
-Now that you know the two numbers create your two brackets and get ready to FACTOR! :)
( n + 8) (n + 6)
-The 8 and 6 were placed here because 8(6)= 48 and 8+6=14
- These n's were put here
because n(n) is n² from
our equation before

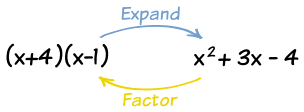
Standard Form to Vertex Form
Standard Form: 0= ax² + bx + c
Vertex Form: y=a(x-h)²+k
0= x² + 6x + 8
-Well first check to see if this is a perfect square because vertex form is a perfect square trinomial.
x(x) = x² 4(2)= 8 4+2= 6
(x + 2) ( x + 4)
*This isn't a perfect sqaure because if it were then both the brackets would have the same numbers and could be just written as (x+s)²
-To turn his into a perfect sqaure then you have to divide the b value by 2 and sqaure it (this always works)
*In this case the b value is 6
6/2=3 3²=9
-Now we have to take the answer and put it into our equation
x² + 6x + 9 - 9 + 8
*We have to subtract the 9 right after because we can't actually change the equation
-Factor only the "x² + 6x + 9"
x(x)= x² 3(3)= 9 3+3+ 6
(x + 3) (x + 3) = (x + 3)² *PERFECT SQUARE
-Collect the like terms
(x + 3)² -9 + 8
= (x + 3)² - 1
-Put your equation together
y= (x + 3)² - 1 *VERTEX FORM

Factored Form to Standard Form
Factored Form: y=a(x-r)(x-s)
Standard Form: 0=ax²+bx+c
(x + 8) (x + 3)
-Expand the brackets
x(x)= x² x(3)= 3x 8(x)= 8x (8)(3)= 24
x² + 3x + 8x + 24
-Collect like terms
x² + 11x + 24
Standard form:
0= x² + 11x + 24
Vertex Form to Standard Form
Standard Form: 0= ax² + bx + c
Vertex Form: y= a(x-h)2 + k
y= 3(x-2)² + 1
-Get rid of the square
y= 3(x-2)(x-2) + 1
-Expand into Brackets
y= (3x-6)(x-2) + 1
-Expand the brackets
3x(x)= 3x² 3x(-2)= -6x -6(x)= -6x -6(-2)= 12
3x² - 6x - 6x + 12
-Collect like terms
3x² - 12x + 12
Standard Form: 0= 3x² - 12x + 12

